Software

Software available here are for educational or academic use only. All rights of reproduction or
distribution in any form are reserved.

PolyDyna
PolyDyna is an extended version of PolyTop that solves topology optimization problems for structures subjected to dynamics loads.
PolyStress
PolyStress is an extended version of PolyTop that solves stress constrained mass minimization considering linear and material nonlinear problems. It uses an augmented Lagrangian approach to handle local stress constraints.
PolyTop3D
PolyTop3D is an extended version of PolyTop that uses a virtual element method (VEM)-based topology optimization framework using polyhedral elements, which can handle any non-Cartesian design domain, to solve three dimensional topology optimization problems.
PolyMat
PolyMat is an extended version of PolyTop that can accommodate and arbitrary number of candidate materials and an arbitrary number of volume constraints. The volume constraints can be specified to control any subset of the candidate materials and any subregion of the domain.
MERLIN 2
MERLIN2 is an extended version of the MERLIN software with significant improvement. The MERLIN2 software offers implementation of the N5B8 model, new triangulation schemes for polygonal panels, convenient import/export capabilities, displacement loading, and improved visualization.
MERLIN
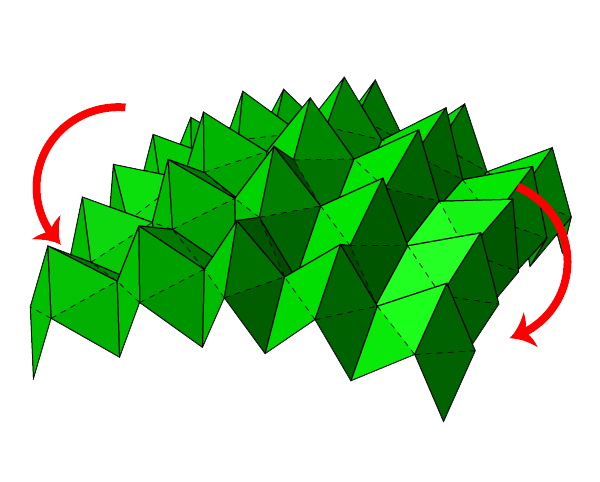
Merlin uses nonlinear mechanics to model large global displacements of non-rigid origami using a reduced representation of the origami.
Fluid Flow Topology Optimization: PolyTopFluid
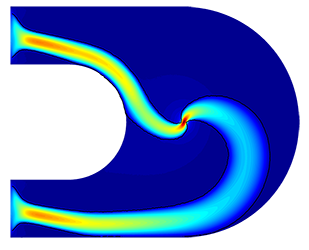
PolyTopFluid is an efficient Matlab code for topology optimization of fluid flow problems.
Topology Optimization for Additive Manufacturing: TOPSlicer
TOPslicer is a simple graphical tool to slice three–dimensional density–based topology optimization data. In addition, the user can change the isosurface cutoff value and evaluate the change on the fly. For problems where symmetry was exploited, TOPslicer can mirror the results in one or more coordinate axis to recover the complete model. Finally, once the cutoff and symmetry conditions have been applied, and the solution is deemed acceptable from inspection, the isosurface can be exported to X3D and/or STL.
GRAND3
GRAND3 — GRound structure Analysis and Design in 3D is an extension of the previous 2D educational MATLAB code for structural topology optimization with discrete elements using the ground structure approach. Domains can be concave and with the possibility of holes. Concavities and holes are handled by defining collision zones (or hitboxes). Both, the domain and the collision zones are procedurally generated, thus allowing for simplicity and flexibility in the analysis.
GRAND

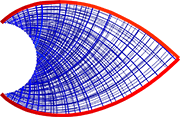
GRAND — GRound structure Analysis and Design is an educational MATLAB code for structural topology optimization with discrete elements using the ground structure approach. Domains can be concave and with the possibility of holes. Concavities and holes are handled by defining collision zones (or hitboxes). Both, the domain and the collision zones are procedurally generated, thus allowing for simplicity and flexibility in the analysis.
PolyMesher
In topology optimization, polygonal discretizations have been shown not to be susceptible to numerical instabilities such as checkerboard patterns. We have developed a simple and robust Matlab code for polygonal mesh generation, called PolyMesher.
PolyTop
PolyTop is an efficient Matlab code for structural topology optimization that includes a general finite element routine based on isoparametric polygonal elements.
2D ABAQUS UEL for the PPR potential-based cohesive model

The PPR potential-based cohesive zone model is implemented in a commercial software, i.e. ABAQUS, as a user-defined element (UEL) subroutine. The source code of the UEL subroutine is provided for a two-dimensional linear cohesive element for educational purposes.
3D ABAQUS UELs for the PPR potential-based cohesive model


The PPR potential-based cohesive zone model is implemented in a commercial software, i.e. ABAQUS, as a user-defined element (UEL) subroutine. The source code of the UEL subroutine is provided for a small library of three-dimensional cohesive elements, i.e. linear brick elements, linear tetrahedral elements, and quadratic tetrahedral elements, for educational purposes.
NLS++: A unified library of nonlinear solution schemes
Nonlinear problems are prevalent in structural and continuum mechanics, and there is high demand for computation tools to solve these problems. The governing finite element equations and constraint equation for various solution schemes are combined into a single matrix equation. This theoretical model leads naturally to an effective object-oriented implementation.
BEAN: Boundary Element ANalysis
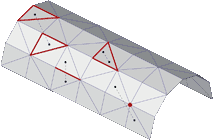
Symmetric Galerkin Boundary Element Method presents an introduction as well as recent developments of this accurate, powerful, and versatile method. The formulation possesses the attractive feature of producing a symmetric coefficient matrix. In addition, the Galerkin approximation allows standard continuous elements to be used for evaluation of hypersingular integrals.
Development of user subroutines in commercial software (UMAT and UEL in ABAQUS)

ABAQUS allows user to add user subroutines to achieve specific functionalities. This material subroutine UMAT is implements graded elements with variable conductivity in ABAQUS. It can incorporate any functional variation of heat conductivity and specific heat.

Reference: A. Sutradhar and G. H. Paulino. "A simple boundary element method for potential problems in nonhomogeneous media". International Journal for Numerical Methods in Engineering Vol. 60, pp. 2203-2230, 2004.

Click here to download User Subroutine.

Integration of singular enrichment functions in the generalized/extended finite element method
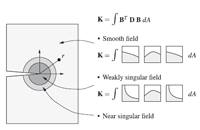
A mapping method is developed to integrate weak singularities, which result from enrichment functions in the generalized/extended finite element method. The integration scheme is applicable to 2D and 3D problems including arbitrarily shaped triangles and tetrahedra. Implementation of the proposed scheme in existing codes is straightforward. Numerical examples for 2D and 3D problems demonstrate the accuracy and convergence properties of the technique.